Traffic jams seem to form magically: often, there is no obvious reason for the slowing down, but nevertheless traffic flow jams spontaneously. In fact, such jamming phenomena in traffic can happen due to collective effects: at some density of cars, their interactions to keep sufficient distance and avoid collisions are sufficient to collectively slow them down.
We elucidate these collective effects in traffic using physical models. This collective jamming reminds a lot of the dynamic slow down in supercooled liquids and glasses, where a liquid, quenched below its freezing point becomes increasingly viscous until it appears like a solid. In this “amorphous solid”, spectacular slow down of the atomic dynamics occurs due to the high atomic density that frustrates the atoms and makes them “freeze” from a liquid into a jammed solid.
To obtain insight into these dynamic arrest phenomena in traffic flow, we use a simple simulation model (the “Nagel-Schreckenberg model”), in which cars move unidirectionally along a single lane, accelerating up to some maximum speed and breaking if there is a car in front. We observe that locally, jamming happens spontaneously, see Figure 1 below. We use this simple simulation model to ask questions like: Why do traffic jams form, and how can they arise without any obvious obstacle? What is the physical nature of this jamming phenomenon?
Using dynamic correlation functions, we measure correlations in the motion of cars. These allow us to determine the dynamic susceptibility: like a magnet that reacts to external magnetic fields, the flow within the highly correlated traffic reacts to small dynamic perturbations. In analogy with the magnet, for which the susceptibility indicates how many spins align spontaneously, we can hence define a dynamic susceptibility that indicates how many cars move collectively. We indeed find increasing dynamic susceptibility with increasing density of cars, see Figure 2 below. We thus apply tools from equilibrium statistical physics to describe dynamic quantities, as has been developed in the field of glasses.
As a result, we find that indeed correlations grow strongly with density. This growth of correlations and dynamic susceptibility highlights the collective effects in traffic, and indicates that jams can indeed form spontaneously. Surprisingly, we find that in the limit of strong breaking, the dynamic susceptibility even diverges, indicating a true dynamic phase transition. See our paper in Phys. Rev. Lett. (2012) for a complete description. This second-order like transition indicates the beginning of a phase-separated region, where strongly jammed traffic coexists with free traffic flow, see paper in Phys. Rev. E (2014).
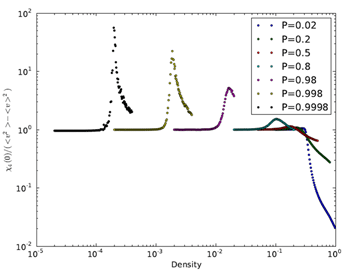
Dynamic susceptibility as a function of density of cars for different fluctuation parameters P of the Nagel-Schreckenberg model. P indicates the probability of braking, and 1-P the probability of acceleration. The emerging sharp peak of the dynamic susceptibility indicates the strong susceptibility of traffic flow to fluctuations, see paper in Phys. Rev. Lett.
