The curvature dependence of the surface tension is central to the nucleation of liquids, but remains difficult to access experimentally and predict theoretically. This curvature dependence arises from the curvature-dependent molecular structure, which, for small nuclei, can deviate significantly from that of the planar liquid interface.
We employ critical Casimir forces to finely adjust colloidal particle interactions and induce liquid nucleation, and image individual nuclei at the particle scale to measure their curvature-dependent surface tension directly from thermally excited surface distortions. Using continuum models, we elucidate the interplay between nucleus structure, particle pair potential, and surface tension. Our results reveal a 20% lower surface tension for nuclei of critical size
compared to bulk liquids, leading to 3 orders of magnitude higher nucleation rates, thus highlighting the importance of surface tension curvature corrections for accurate prediction of nucleation rates.
See our paper in PRL (2018)
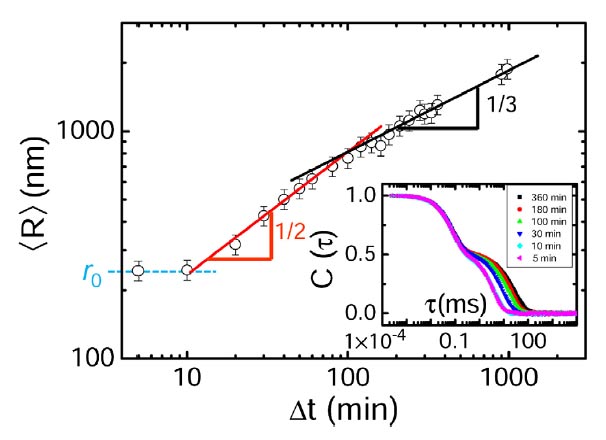
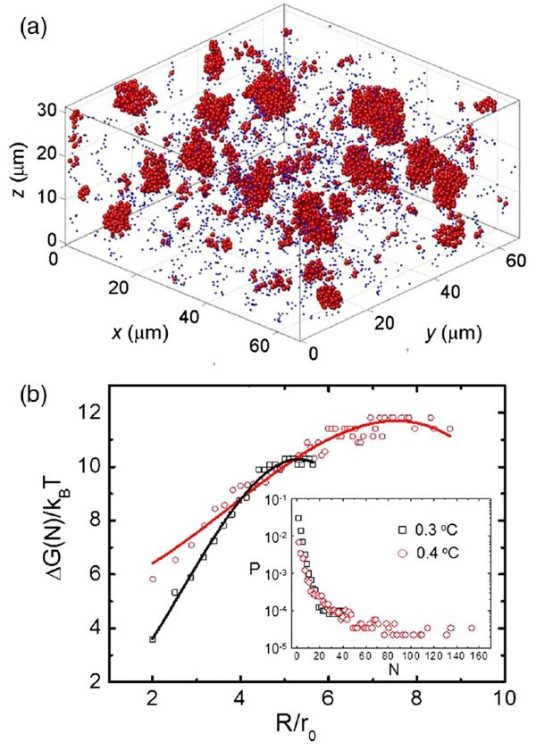
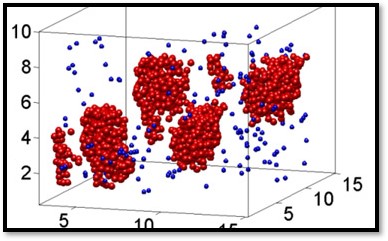
The similarity of our colloidal liquid nucleation and conventional nucleation in molecular liquids is already witnessed in the growth of the liquid nuclei, see Fig. 1. We measure the average radius R of the growing nuclei by dynamic light scattering and find that it exhibits three regimes: constant radius, growth with R ∝ t1/2, and growth with R ∝ t1/3. These regimes indicate the delay due to nucleation, surface limited growth, and diffusion-limited growth, respectively. Indeed, three-dimensional reconstructions made by confocal microscopy show a number of super- and subcritical nuclei, see Fig. 2 and picture above. By assuming a Boltzmann distribution in nucleation equilibrium, we can use the size distribution to determine the Gibbs free energy of nucleation as a function of size, which shows the typical energy barrier associated with nucleation, see Fig. 2. Here, we have studied two different particle attractions; the lower attraction leads indeed to a larger activation barrier as expected. We can thus finely adjust the amount of supercooling by tuning the critical Casimir force.

Reconstruction of a critical colloidal liquid nucleus. Big red particles have more than four neighbors, small blue particles less neighbors, making the nucleus visible.
Looking in more detail, the nuclei exhibit elliptical shape to first order, i.e. they deviate from the spherical lowest-energy state due to thermal fluctuations. We use the statistics of these thermal distortions to determine, for each nucleus radius its effective surface tension. This allows us to plot the surface tension as a function of radius, see Fig. 3. We observe a reduction of ~20% with respect to the surface tension of the flat interface, which will lead to a ~7 orders of magnitude higher nucleation rate (as it enters exponentially in the classical nucleation theory expression). The curvature dependence of the surface tension due to distortion of the molecular structure at the curved interface is thus important to take into account for prediction of nucleation rates.