Statistical physics has been very successful in deducing macroscopic properties of materials from the interactions between their microscopic components. Active matter systems, on the other hand, such as active colloids, animal flocks, or cytoskeletal assemblies, are prone to develop out-of-equilibrium patterns. These spatial heterogeneities are essential to life processes. Cells are typically crowded by many motor proteins of different kind. The collective behavior of these motors is far from being understood. We use a simple simulation model known as Totally Asymmetric Simple Exclusion Process (TASEP) to elucidate patterns of traffic flow in two-dimensional networks.
The particles perform unidirectional motion with random sequential hops, while avoiding overlap (hard-core exclusion): A motor can only advance if there is an unoccupied site in front of it, otherwise no progression occurs.
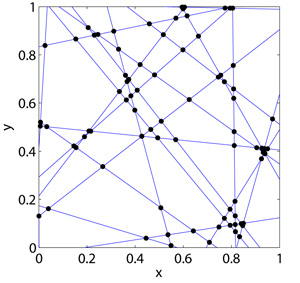
We model cytoskeleton networks with a two-dimensional network of intersecting strands (Fig. 1), inspired by actual networks grown on cover slides in in vitro experiments (Erwin Peterman Lab, Vrije Universiteit). We assume only simple intersections, consisting of two intersecting lines, as in reality, the occurrence of multiple microtubules intersecting at the same point is very unlikely. Because the direction of motion along a microtubule is fixed, we further assume that every intersection has precisely two incoming and two outgoing segments. Such networks can be easily created in simulation by placing straight lines at arbitrary angles into a square, as shown in Fig. 1. The motors can switch lines at the intersections with probability γ.
The simulations show that this switching probability γ at intersections can lead to drastic changes in the transport properties of the system. Surprisingly, we find that asymmetric switching helps to stabilize the total current through the network as it makes it insensitive to the total density of motors. This may help the cell to provide relatively constant transport properties, while the motor density is varying.
For more details, see our paper in Phys. Rev. E (2015)