Check out our paper in Phys. Rev. Lett. (2021)
Limited-valency colloidal particles can self-assemble into polymeric structures analogous to molecules. While their structural equilibrium properties have attracted wide attention, insight into their dynamics has proven challenging. Here, we investigate the polymerization dynamics of semiflexible polymers in 2D by direct observation of assembling divalent particles, bonded by critical Casimir forces. The reversible critical Casimir force creates living polymerization conditions with tunable chain dissociation, association, and
bending rigidity. We find that unlike dilute polymers that show exponential size distributions in excellent agreement with Flory theory, concentrated samples exhibit arrest of rotational and translational diffusion due to a continuous isotropic-to-nematic transition in 2D, slowing down the growth kinetics.
At low density, the colloidal polymers assemble in equilibrium and show the expected length distributions as predicted by Flory theory. This is shown in Fig. 1. With increasing density, their growth deviates increasingly from this length distribution: diffusion and rotation, necessary for linking of new particles or chains become kinetically arrested and the growth comes to a stop. In addition, the growing polymer chains exhibit an isotropic-nematic transition, leading to kinetically arrested domains of parallel chains. The picture above shows the increasing alignment of neighboring chains (highlighted in red) with increasing density. Accordingly, the growing polymer chains exhibit an isotropic-nematic transition, while at the same time their diffusion is blocked leading to arrest of their growth.
These findings are important for biopolymers growing on surfaces and at interfaces.

Figure 1 Colloidal polymer equilibrium
(a,b) Microscope images of colloidal polymers assembled in equilibrium at Casimir temperatures 0.06 and 0.08K below the solvent critical point. (c) Length distributions at different attractive strength, data (connected points) and Flory theory predictions (straight line).
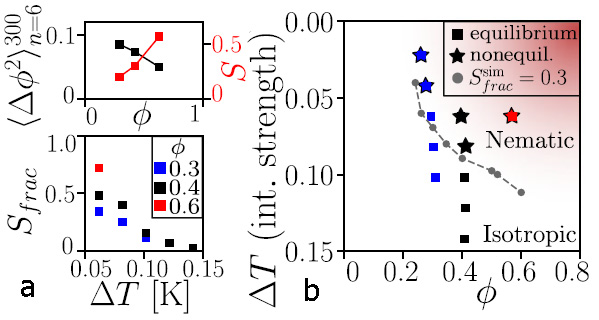
Figure 2 Colloidal polymer alignment and arrest
(a) (top) Mean-square displacement and nematic order parameter (fraction of aligned bonds) as a function of volume fraction; while the alignment increases, the mobility drops. (bottom) Particle fraction with nematic order as a function of Casimir temperature (attractive strength increasing from right to left) for three different volume fractions. (b) Isotropic-nematic phase diagram as a function of volume fraction and Casimir temperature. Squares indicate equilibrium, stars nonequilibrium length distributions. Clearly, their transition delineates the isotropic-nematic phase boundary.
