Check out our paper in Phys. Rev. Materials (2022)
Self-assembling patchy colloidal particles are promising candidates to create designer soft materials. To dress such systems with mechanical functionality, one can take inspiration from biological semiflexible filaments, whose mechanical behavior is central to the cell’s function.
We perform mechanical experiments on analogues of biological filaments, semiflexible “colloidal polymers” made from bonded di-patch colloidal particles, whose bonding strength and persistence length we can adjust in-situ. Using optical tweezers to probe their extreme mechanics under increasingly high compressions, we reveal a rich non-linear mechanical response involving buckling, viscoelastic creep, and ultimately fracture. By characterizing this response using elastic and viscoelastic models involving Euler buckling and stress relaxation, we relate the critical bending at fracture to the finite patch size of the colloids. Our results demonstrate the crucial role of finite patch size in the mechanics of self-assembled colloidal materials, and provide mechanical information essential to design functional colloidal architectures inspired by nature.
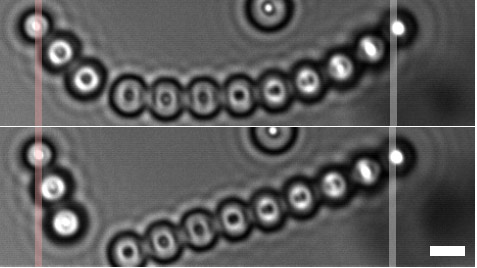
We use the optical tweezers to measure the applied force, and image the resulting buckling of the chain. The force as a function of displacement shows typical Euler buckling behavior, as shown in Fig. 1 below: when the initially sharply rising force reaches a critical threshold, Fc, it suddenly becomes constant upon further compression, indicating buckling of the chain. At the same time, the deflection (first-mode amplitude) increases in a way characteristic for Euler buckling, as shown by the overlap of our data and the dashed line indicating the Euler buckling of an elastic beam in Fig. 1b.
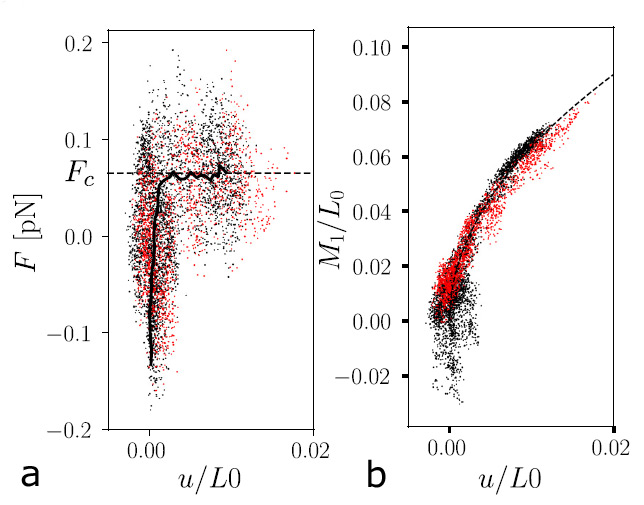
Fig. 1 Euler-buckling response of the colloidal chain
(a) Force-compression curve showing buckling at a critical force Fc, after which the force curve becomes flat, indicating the buckled state. (b) Deflection-compression curve showing how the first-mode amplitude develops with compression u. Both (a) and (b) show the typical Euler buckling behavior of an elastic rod as indicated by the dashed lines.
We also study the slow relaxation of the bent colloidal chain: Upon holding the chain in the buckled configuration, the applied force decreases, while the compression keeps increasing, see Fig. 2. This indicates internal reorganization of the chain most likely due to slow slip of the patchy particle bonds over time. While this process is clearly associated with energy dissipation, as shown by the open loop in Fig. 2a, whose area is a measure of the dissipated energy, the deflection nevertheless shows almost perfect reversibility and only slight deviation from the Euler prediction.
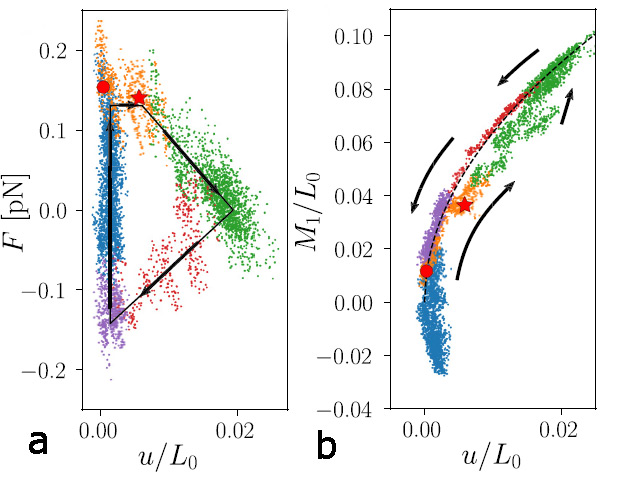
Fig. 2 Relaxation of the buckled chain
Force (a) and first-mode amplitude (b) versus compression for the entire cycle of loading, holding and unloading. After loading (blue data) and buckling (orange), the chain is held by the optical tweezer and relaxes (green). Final unloading leads it back to the initial state (red data). While there is clearly energy dissipation (area of the force-compression cycle in Fig. 2a), the process nevertheless proceeds reversibly as shown by the deflection curve in Fig. 2b.